Abstract

We introduce the Fixed Point Diffusion Model (FPDM), a novel approach to image generation that integrates the concept of fixed point solving into the framework of diffusion-based generative modeling. Our approach embeds an implicit fixed point solving layer into the denoising network of a diffusion model, transforming the diffusion process into a sequence of closely-related fixed point problems. Combined with a new stochastic training method, this approach significantly reduces model size, reduces memory usage, and accelerates training. Moreover, it enables the development of two new techniques to improve sampling efficiency: reallocating computation across timesteps and reusing fixed point solutions between timesteps. We conduct extensive experiments with state-of-the-art models on ImageNet, FFHQ, CelebA-HQ, and LSUN-Church, demonstrating substantial improvements in performance and efficiency. Compared to the state-of-the-art DiT model, FPDM contains 87% fewer parameters, consumes 60% less memory during training, and improves image generation quality in situations where sampling computation or time is limited.

Overview

Fixed Point Diffusion Model (FPDM) is a highly efficient approach to image generation with diffusion models. FPDM integrates an implicit fixed point layer into a denoising diffusion model, converting the sampling process into a sequence of fixed point equations. Our model significantly decreases model size and memory usage while improving performance in settings with limited sampling time or computation. We compare our model, trained at a 256px resolution against the state-of-the-art DiT on four datasets (FFHQ, CelebA-HQ, LSUN-Church, ImageNet) using compute equivalent to 20 DiT sampling steps. FPDM (right) demonstrates enhanced image quality with 87\% fewer parameters and 60\% less memory during training.

Architecture

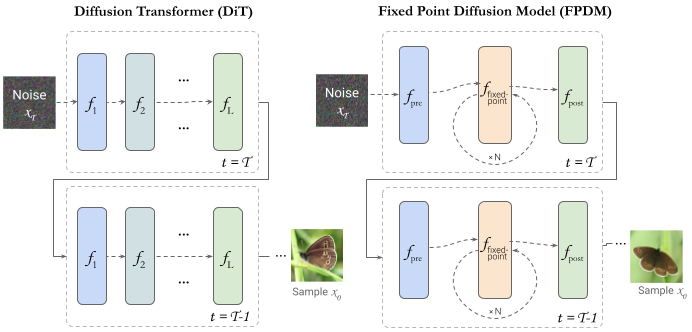
Above we show the architecture of FPDM compared with DiT. FPDM keeps the first and last transformer block as pre and post processing layers and replaces the explicit layers in-between with an implicit fixed point layer. Sampling from the full reverse diffusion process involves solving many of these fixed point layers in sequence, which enables the development of new techniques such as timestep smoothing and solution reuse.

Examples

Random (non-cherry-picked) examples of our method compared to DiT.

Citation

Acknowledgements

L.M.K. is supported by the Rhodes Trust.